Notice that the left side expresses the expansion of sine of double angle, hence the given identity `(2 tan theta)/(1 tan^2 theta ) = sin 2 theta ` is checked Approved by eNotes Editorial TeamI'm having trouble on where to begin proving identities I must prove that 2 tan theta /(1 tan^2 theta) = sin 2theta Hi Charmaine, In a problem like this when I don't immediately see something useful I write everything in terms of sines and cosines and then see if I can manipulate both sides to make them equal$\cos{2\theta}$ $\,=\,$ $\dfrac{1\tan^2{\theta}}{1\tan^2{\theta}}$ A mathematical identity that expresses the expansion of cosine of double angle in terms of tan squared of angle is called the cosine of double angle identity in tangent Introduction Let the theta be an angle of a right triangle

If Theta 30 Verify That Tan 2theta 2 Tan Theta 1 Tan Square Theta Maths Introduction To Trigonometry Meritnation Com
25.quad int(1+tan^(2)x)/(1-tan^(2x)dx equals to
25.quad int(1+tan^(2)x)/(1-tan^(2x)dx equals to- · What is `(2tantheta)/(1tan^(2)theta)` equal to ?$\tan^2{\theta} \,=\, \sec^2{\theta}1$ The square of tan function equals to the subtraction of one from the square of secant function is called the tan squared formula It is also called as the square of tan function identity Introduction The tangent functions are often involved in trigonometric expressions and equations in square form



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf
· What is cos 2 equal to?Click here👆to get an answer to your question ️ Solve (sec^2 theta 1)(1 cosec^2 theta) = 1If tan 2theta tan theta = 1, then the general value of theta is Login Study Materials NCERT Solutions 2 tan 2 θ = 1 – tan 2 If Tan N Theta Equal Tan M Theta Then The Different Values Of Theta Will Be In
Prove the following trigonometric identity $$1 \tan^2\theta = \sec^2\theta$$ I'm curious to know of the different ways of proving this depending on different characterizations of tangent and seIf sec theta = 1 1/4, then tan theta/2 is equal to · $$\cos^{1} \theta \neq \frac{1}{\cos \theta}$$ That is why I prefer to use the arc notation as in $\arccos \theta$ The notations $\cos^{1} \theta$ and $\arccos \theta$ represent the same thing, which is, roughly speaking, the inverse of $\cos \theta$ (although it is not a true inverse since $\cos$ is not injective) Back to your question
Given that Tan ¢ 1/ Tan ¢ = 2 On squaring both sides we get, ( Tan ¢ 1/Tan ¢ )² = (2)² We know that, ( A B)² = ( A)² ( B)² 2 × A × B ( Tan² ¢ ) ( 1/Tan² ¢ ) 2 × Tan ¢ × 1/Tan ¢ = 4 ( Tan² ¢ ) ( 1/Tan² ¢ ) 2 = 4 ( Tan² ¢ ) ( 1/Tan² ¢ ) = 42Select the correct option from the given alternatives If θ = 60°, then 1tan2θ2tanθ is equal toYou can use this fact to help you keep straight that cosecant goes with sine and secant goes with cosine The following (particularly the first of the three below) are called "Pythagorean" identities sin 2 (t) cos 2 (t) = 1 tan 2
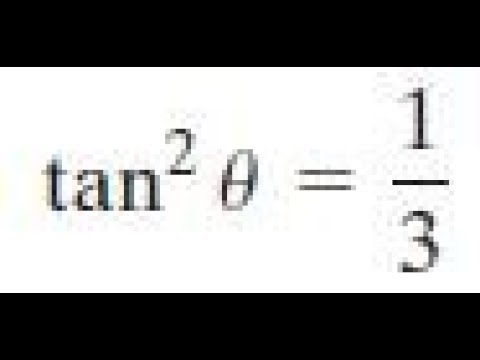


Tan 2 Theta 1 3 Solve For Interval 0 Less Theta Less 2pi Youtube



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorWhen you use this particular substitution, keep in mind that 1 plus the tangent squared of theta is equal to the secant squared of theta (1 tan^2(theta) = sec^2(theta)) This is a trig identityIf on the other hand, you have a function that depends on some constant squared minus x ^2, you might want to consider the substitution x equals C times the sine of theta ( x = C * sin( theta ))Here is another way to proceed $\displaystyle\int\frac{\tan^4\theta}{1\tan^2\theta}d\theta=\int\frac{\tan^4\theta1}{1\tan^2\theta}d\theta\int\frac{1}{1\tan^2



Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Th
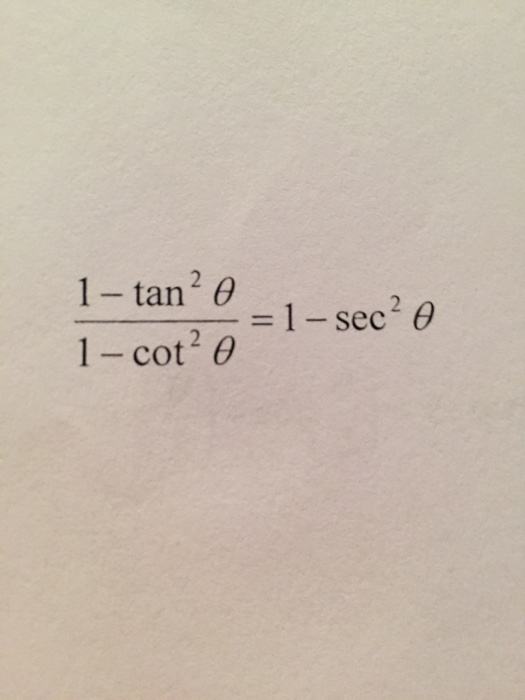


Solved 1 Tan 2 Theta 1 Cot 2theta 1 Sec 2theta Ve Chegg Com
⇒ tan 2 θ = cot θ ⇒ 1 − tan 2 θ 2 tan θ = tan θ 1 ⇒ 2 tan 2 θ = 1 − tan 2 θ ⇒ tan 2 θ = 3 1 ⇒ tan θ = ± 3 1 ∴ θ = ± 6 πStep by step solution by experts to help you in doubt clearance & scoring excellent marks in exams0 given tan2θ = 2tan2ϕ1 ⇒ 1tan2θ = 2(1tan2ϕ) (1) now, cos2θ sin2ϕ = 1tan2θ1−tan2θ 1− 1tan2ϕ1 = 1tan2θ1−tan2θ



Tan Theta Tan 2theta Tan3 Theta 0 Maths Trigonometric Functions Meritnation Com



Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
· If Tan Theta Plus I Phi Sin X Plus Iy Then The Value Of If Tan Theta Sin Theta M And Tan Theta Sin Theta N Then If Tan Thetadfrac43 Then Sin Theta Is If Tan X B A Then The Value Of A Cos 2x B Sin 2x Is If tan1 (a / x) tan1 (b / x) = π / 2, then x is equalPrave That If Tan θ 1 Tan θ = 2 , Then Show that Tan 2 θ 1 Tan 2 θ = 2 · In mathematics an identity is an equation that is always true Meanwhile trigonometric identities are equations that involve trigonometric
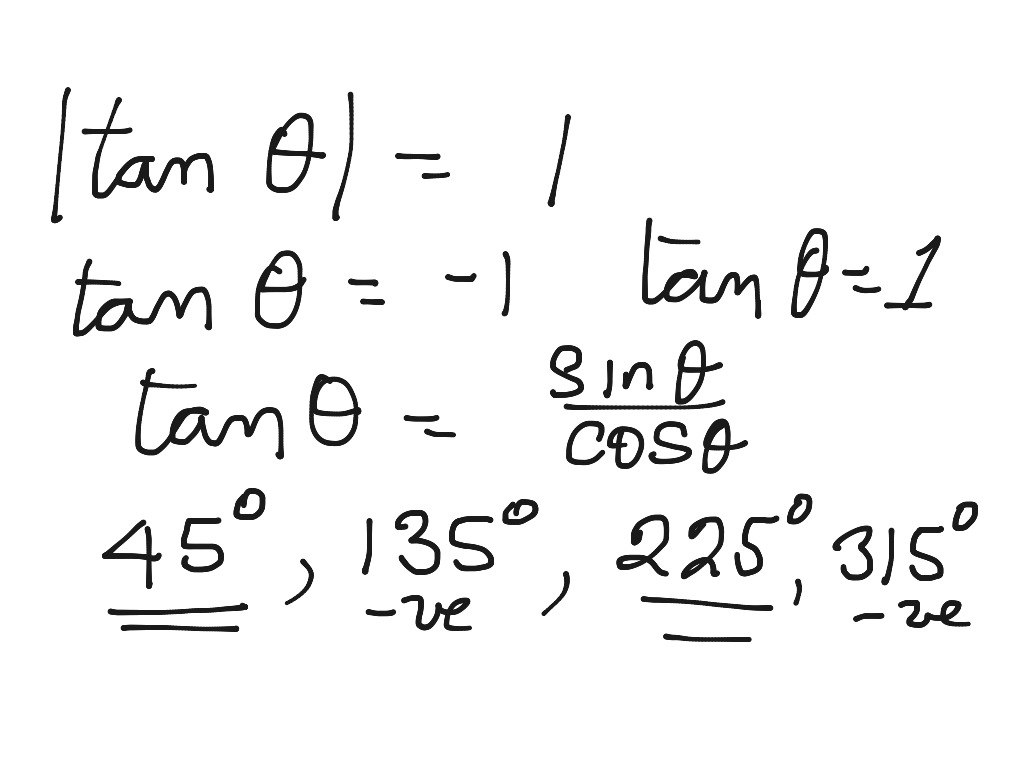


Tan Theta Equals Plus Or Minus 1 Solution Math Trigonometry Showme
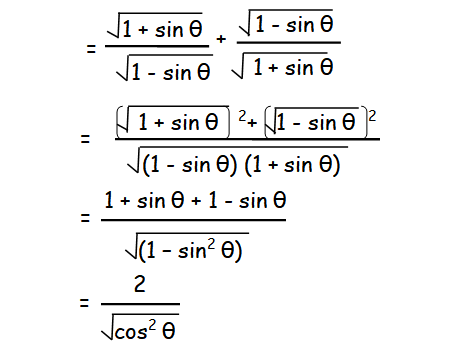


Proving Trigonometric Identities
Free math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantly= (1 tan 2 θ) / (cot 2 θ 1) Formula for tan Trigonometric ratios of 90 degree minus theta Trigonometric ratios of 90 degree plus theta Trigonometric ratios of angles greater than or equal to 360 degree Trigonometric ratios of complementary anglesFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor



If Left Theta 60 Circ Text Then Frac 1 Tan 2 Theta 2 Tan Theta Text



Prove That 1 Tan Theta Tan 2theta Sec 2theta
`(sin^2 theta 1/(1 tan^2 theta ))` = `( sin^2 theta 1/(sec^2 theta))` =`( sin^2 theta cos^2 theta)` =1If ` sin theta = cos theta` ,then the value of `2 tan^(2) theta sin^(2) theta 1` is equal toUPSEE 18 If (1 tan 1°)(1 tan 2°) (1 tan 45°) = 2n, then n is (A) 22 (B) 24 23 (D) 12 Check Answer and Solution for ab


Solution Prove That Sin Theta Times Cos Theta Divided By Cos 2 Theta Sin 2 Theta Tan Theta Divided By 1 Tan Theta Show Step By Step How To Change The Left To Equal The Right Side Of E
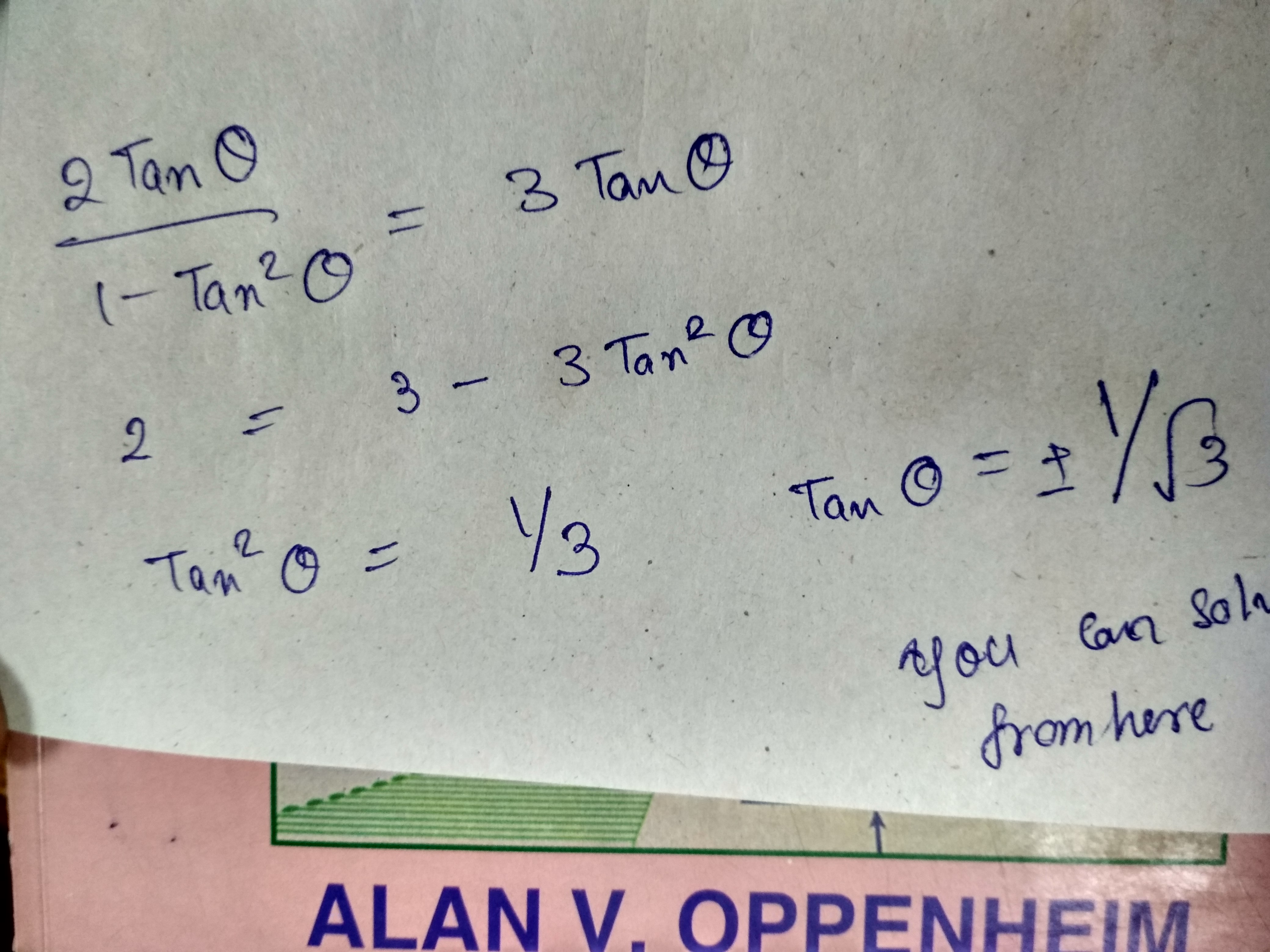


Tan 2theta Equal To 3 Tan Theta Solve To Get Theta Askiitians
If tan1(cotθ) = 2θ, then θ is equal to (A) (π/3) (B) (π/4) (π/6) (D) None of these Check Answer and Solution for above question from Mathe Tardigrade · Using the identities 1 tan2θ = sec2θ 1 secθ = cosθ tanθ = sinθ cosθ sin2θ = 1 −cos2θ 2cos2θ − 1 = cos2θ Start 1 − tan2θ 1 tan2θ = 1 − tan2θ sec2θ =1 tan^2theta1 cot^2theta is equal to
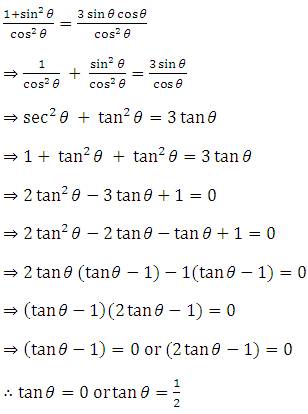


1 Sin2 Theta 3 X Sin Theta X Cos Theta Introduction To Trigonometry Maths Class 10



5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download
(1 − sin 2 θ) (1 tan 2 θ) = cos 2 θ × sec 2 θ = cos 2 θ × cos 2 θ 1 = 1(d/dx) cosec1((1x2/2x)) is equal to (A) (2/1x2), x ≠0 (B) (2(1x)/1x2), x ≠0 (2(1x2)/(1x2)1x2), x ≠±1, 0 (D) None of these CheckSimplify (tan^2 theta 1)/(tan^2 theta) csc2 theta –1 tan2 theta 1 ~ 4) Use a sum or difference identity to find the exact value of sin 15° (sqrt)2 (sqrt)6/ 4 If sin theta is equal to 5/13 and theta is an angle in quadrant II find the value of cos theta, sec theta, tan theta, csc theta, cot theta


Solved 1 Tan Theta Tan Theta 1 Cos 2 Theta 1 Tan 2 Chegg Com



Trigonometric Identities Trigonometry Siyavula
If tan2 θ = 2 tan2 φ 1, then cos 2 θ sin2 φ is equal to Q If $\tan^2 \, \theta = 2 \, \tan^2 \, \phi 1,$ then $\cos \, 2 \theta \sin^2 \, \phi $ is equal toI need to prove that $\frac{1\tan^2\theta}{1\cot^2\theta}= \tan^2\theta$ I know that $1\tan^2\theta=\sec^2\theta$ and that $1\cot^2\theta=\csc^2\theta$, making it now $$\frac{\sec^2\theta}{\csc^2\theta,}$$ but I don't know how to get it down to $ \tan^2\theta$Here, $ x $ denotes the greatest integer less than or equal to $ x $ Given that $ f(x) = x x $ The value obtained when this function is integrated with respect to $ x $ with lower limit as $ \frac{3}{2} $ and upper limit as $ \frac{9}{2} $ , is



1 1 Tan Theta 1 Cot Theta 2 Sec 2 Mathematics Topperlearning Com Ggw6mtpp



Tangent Half Angle Formula Wikipedia
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If `tan theta=1/2` and `tan phi =1/3`, then the value of `theta phi` is



Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic



Prove That 1 1 Tan 2 Theta 1 1 Cot 2 Theta 1



Prove That 1 Tan 2 Theta 1 Cot 2 Theta 1 Tan Theta 1 Cot Theta 2 Brainly In



Two Solutions Of Tan 2 8 12 0 45 Corresponding To H ǫ Equals To Download Scientific Diagram


How Do You Prove 1 Sin 2theta 1 Cot 2theta Cot 2theta Socratic
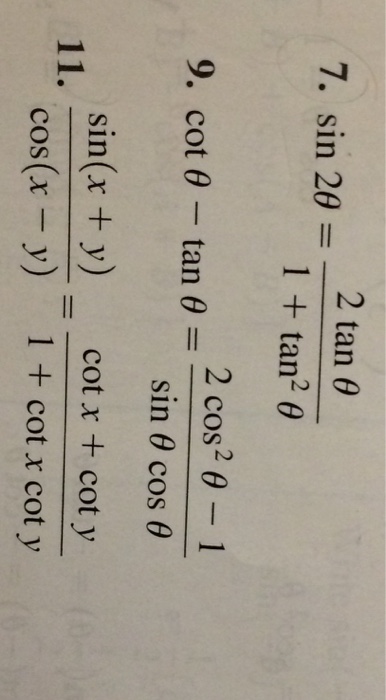


Solved Sin 2 Theta 2 Tan Theta 1 Tan 2 Theta Cot Thet Chegg Com



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf


5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download



Using Trigonometric Identities Problem 3 Trigonometry Video By Brightstorm



Tangent Half Angle Formula Wikipedia


Prove That Math Tan 2 Theta 1 Sec 2 Theta Math Quora



Trigonometric Identities List Of Trigonometric Identities Examples



Revision Trigonometry Siyavula


Prove That Math Tan 2 Theta 1 Sec 2 Theta Math Quora


Prove That Tan 8 1 Cot 8 Cot 8 1 Tan 8 1 Tan8 Cot 8 Studyrankersonline



Proof Tan 2 1 Sec 2 Youtube



If Theta 60 Then 1 Tan 2 Theta 2tan Theta Is Equal To
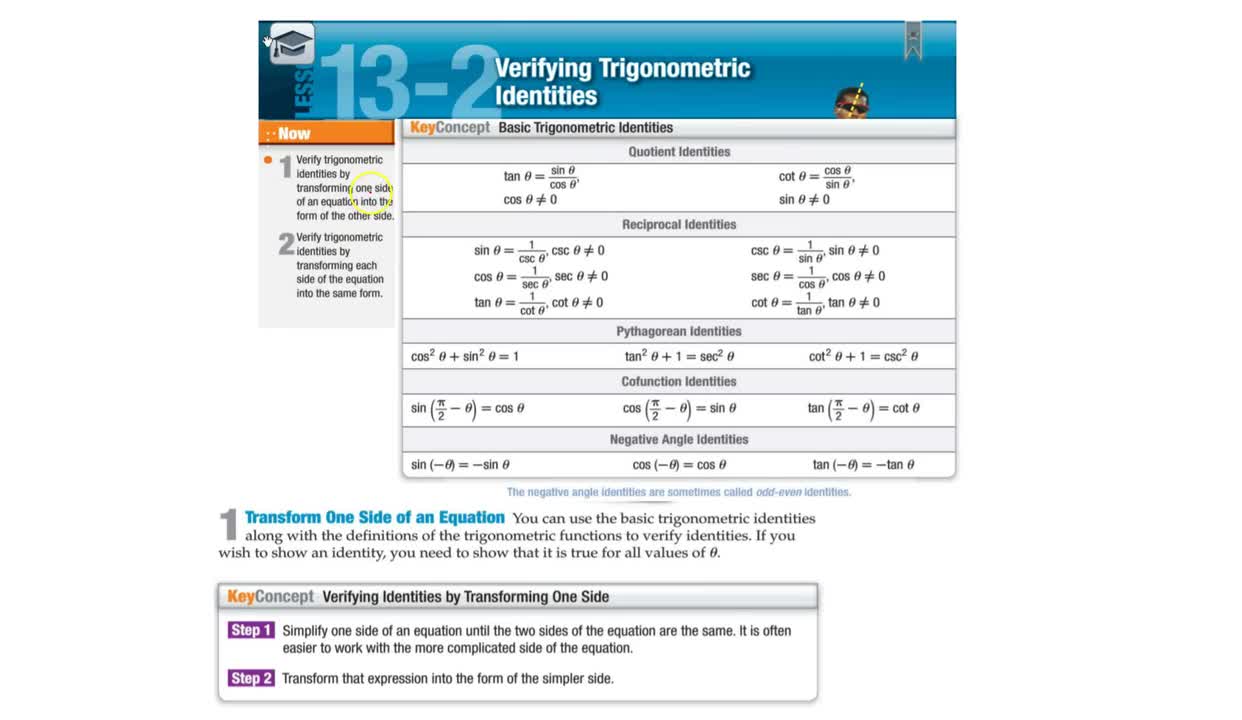


Honors Algebra 2 Trig Notes Chapter 13 Section 2 Bishop Amat Memorial High School



How To Use Double Angle Identities Studypug



Sec 2 Theta 1 Tan 2 Theta Youtube


Trig Identity Reference Article Khan Academy



1 Tan 2 Theta Sin2theta


If Tan Theta Cot Theta 2 Then What Is The Value Of Tan Squared Theta Cot Squared Theta Equal To Quora



Solved 1 Tan Squared Theta Into 1 Cot Square Theta Is Equals To 1 By Sin Squared Theta Minus Sin Brainly In



1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube



Prove That Cot 8 Tan 8 2 Cos 2 8 1 Sin 8 Cos 8


How Do You Verify Tan 28 Sin 28 Tan 28sin 28 Socratic
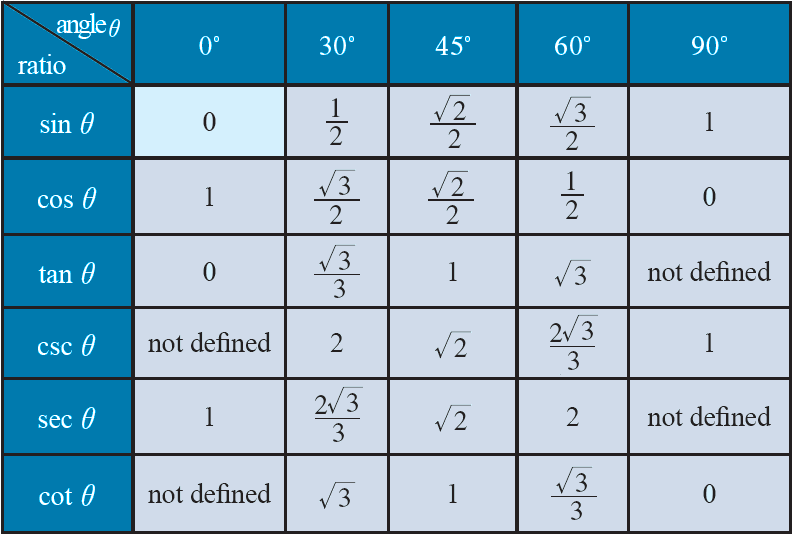


Trigonometric Identities



Tan Theta 1 Tan 2 Theta 2 Cot Theta 1 Cot 2 Theta 2 Sin Theta Cos Theta Brainly In
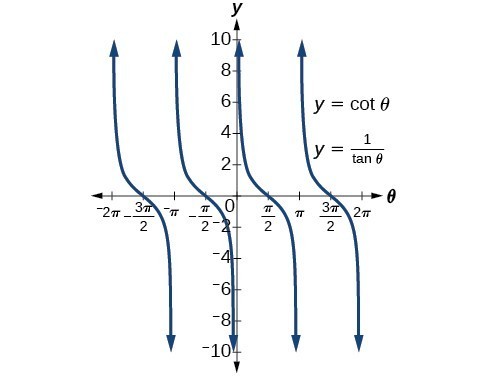


Solving Trigonometric Equations With Identities Precalculus Ii



Solved Establish The Identity 1 Tan 2 Theta 1 Tan 2 Chegg Com
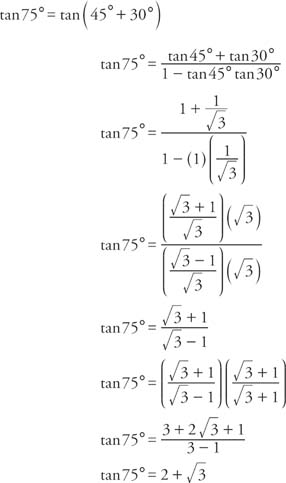


Tangent Identities


If M Cos8 Sin8 And N Cos8 Sin8 Then Show That M N N M 2 1 Tan 2 8 Sarthaks Econnect Largest Online Education Community
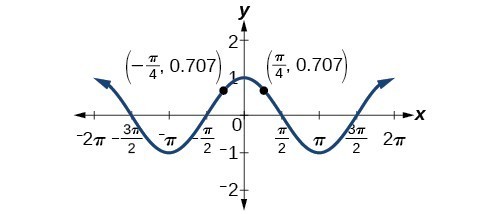


Solving Trigonometric Equations With Identities Precalculus Ii
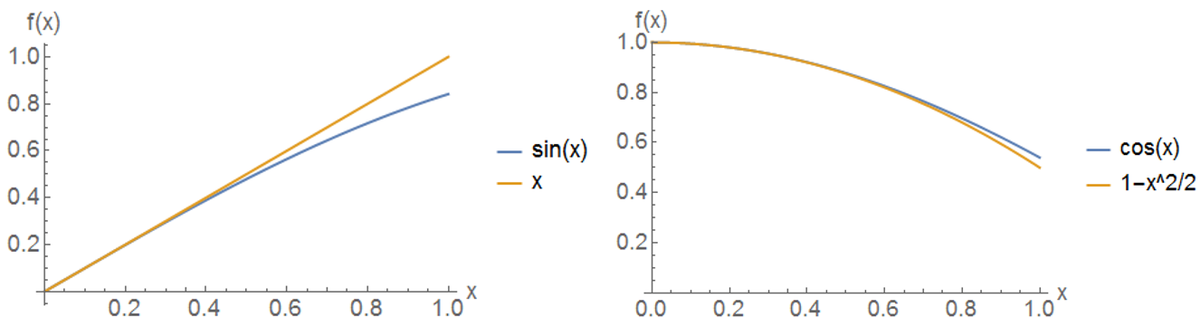


Small Angle Approximation Brilliant Math Science Wiki



Prove That Tan 2 Theta 1 Tan 2 Theta Cot 2 Theta 1



Using Trigonometric Identities Video Khan Academy



Solved Write The Value Of Sin2 8 Cos2 8 1 Tan2 81 Cot2 8 Self Study 365



Prove That 1 Tan Theta Tan 2theta Sec 2theta Youtube



If Tan Theta Sec Theta 2 Then What Is Tan Theta Is Equal To Quora



If 1 Sin 3 Sin Cos Then Show That Tan 1 Or 1 2 Mathematics Topperlearning Com 328h6ymm



If Theta 30 Verify That Tan 2theta 2 Tan Theta 1 Tan Square Theta Maths Introduction To Trigonometry Meritnation Com



Prove That Tan 2 Theta Sin 2 Theta Tan 2 Theta Sin 2 Theta
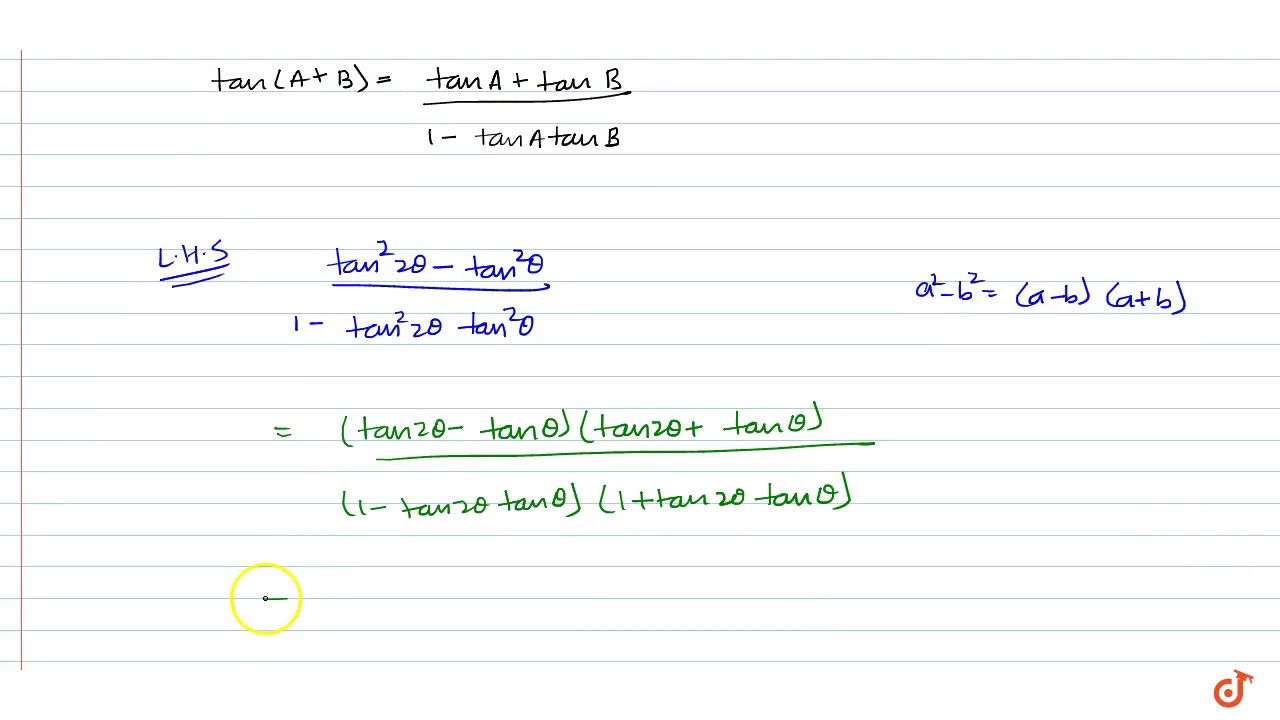


Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Theta Tan 3theta Tan Theta Youtube



14 If Tan 2 Theta Tan Theta 1 Then Theta Is Equal To A Cap Pi Frac 1 6 Mathrm C 2 Mathrm N Pi Pm Frac 1 0 B N Pi Pm Frac 6 D None Of These


If Tan 8 1 Tan 8 2 What Is The Values Of Tan 8 1 Tan 8 Quora


The Trigonometric Ratios Of Angl



Sin 2 Theta Is Equal To 2 Tan Theta Upon 1 Tan Square Theta And Theta 30 Degree Brainly In



Summary Of Trigonometric Identities


Prove That Math Tan 2 Theta 1 Sec 2 Theta Math Quora



Prove That 1 Tan 28 1 Cot 28 1 Tan8 1 Cot8 2 Tan 28



What Is The Value Of Sin 2theta 1 1 Tan 2theta
x-1=sec(squared)x.jpg)


10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com



Tan 2 Theta Cos 2 Theta 1 Cos 2 Theta Brainly In


Tan Theta Equals 0 General Solution Of The Equation Tan 8 0 Tan 8 0



Tan 4 Theta 4 Tan Theta 1 Tan 2 Theta 1 6 Tan 2 Theta Tan 4 Theta Maths Trigonometric Functions Meritnation Com



Trigonometric Identities Ppt Download



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



Solved Prove The Following Identities Tan 2theta 2 Tan Chegg Com


Solving Trigonometric Equations With Identities Precalculus Ii



Art Of Problem Solving
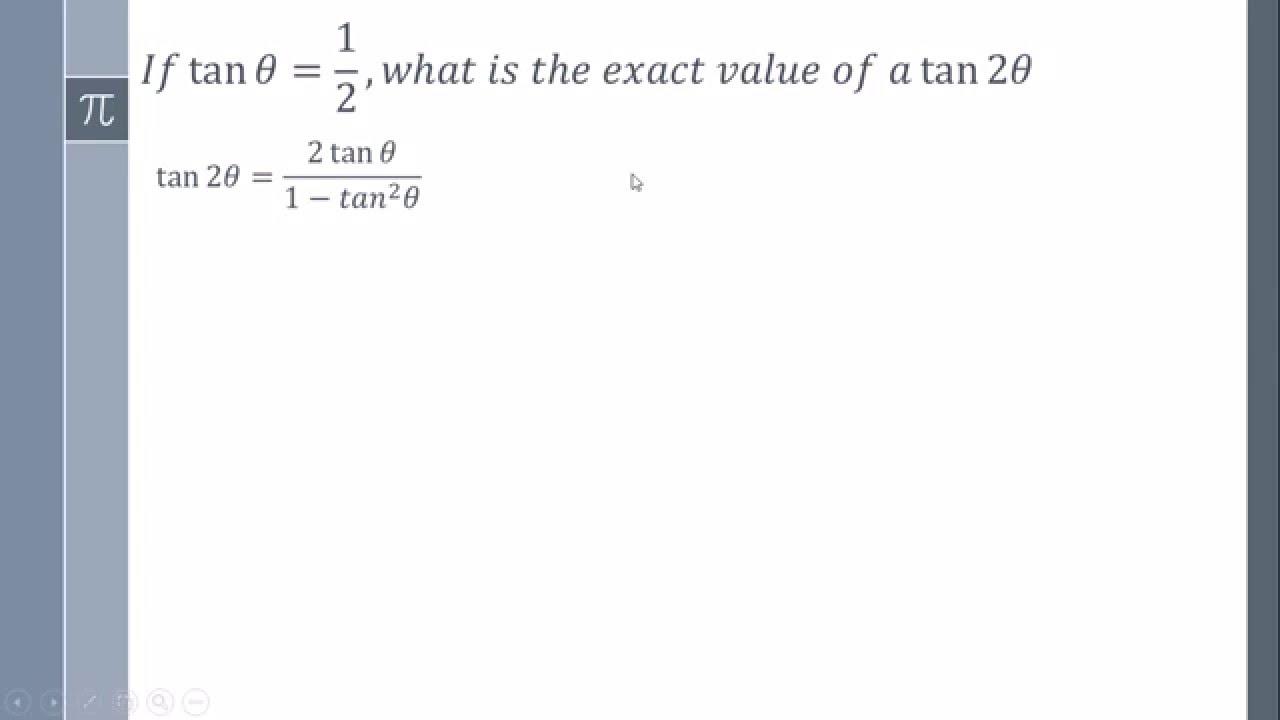


If Tan Of Theta Is 1 2 What Is The Exact Value Of Tan 2 Theta Youtube



If Tan Theta 1 Tan Theta 2 Find The Value Of Tan2theta 1 Tan2theta Maths Meritnation Com


If Tan 8 1 2 And Tan ϕ 1 3 Then The Value Of 8 ϕ Is Studyrankersonline



5 1 Fundamental Trig Identities Reciprocal Identities Sin



Tan Theta Sec Theta 2tan Theta 0 Wyzant Ask An Expert



If Tan 2 Theta 1 2 Tan 2 Phi Prove That Cos 2 Phi 1 2 Cos 2



Trigonometric Identities



How Do You Prove Tan 2x Secx 1 1 Secx Socratic


What Is Tan Squared Equal To


The Trigonometric Ratios Of Angl



1 1 Tan 2 Theta 1 1 Cot 2 Theta 1 Sin 2 Theta Sin 4 Theta Brainly In


Prove That 1 Tan 2 8 1 Cot 2 8 1 Tan 8 Cot 8 2 Tan 2 8 Sarthaks Econnect Largest Online Education Community



If Tan Theta 1 3 Then Evaluate Cosec 2 Theta Sec 2 Theta Cosec 2 Theta Sec 2 Edurev Class 10 Question



Trigonometry Reciprocal Identities Expii
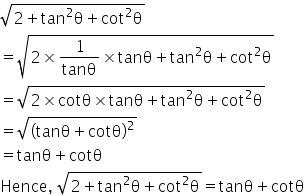


Prove That 2 Tan2 Cot2 Tan Cot Mathematics Topperlearning Com Ttevdk55
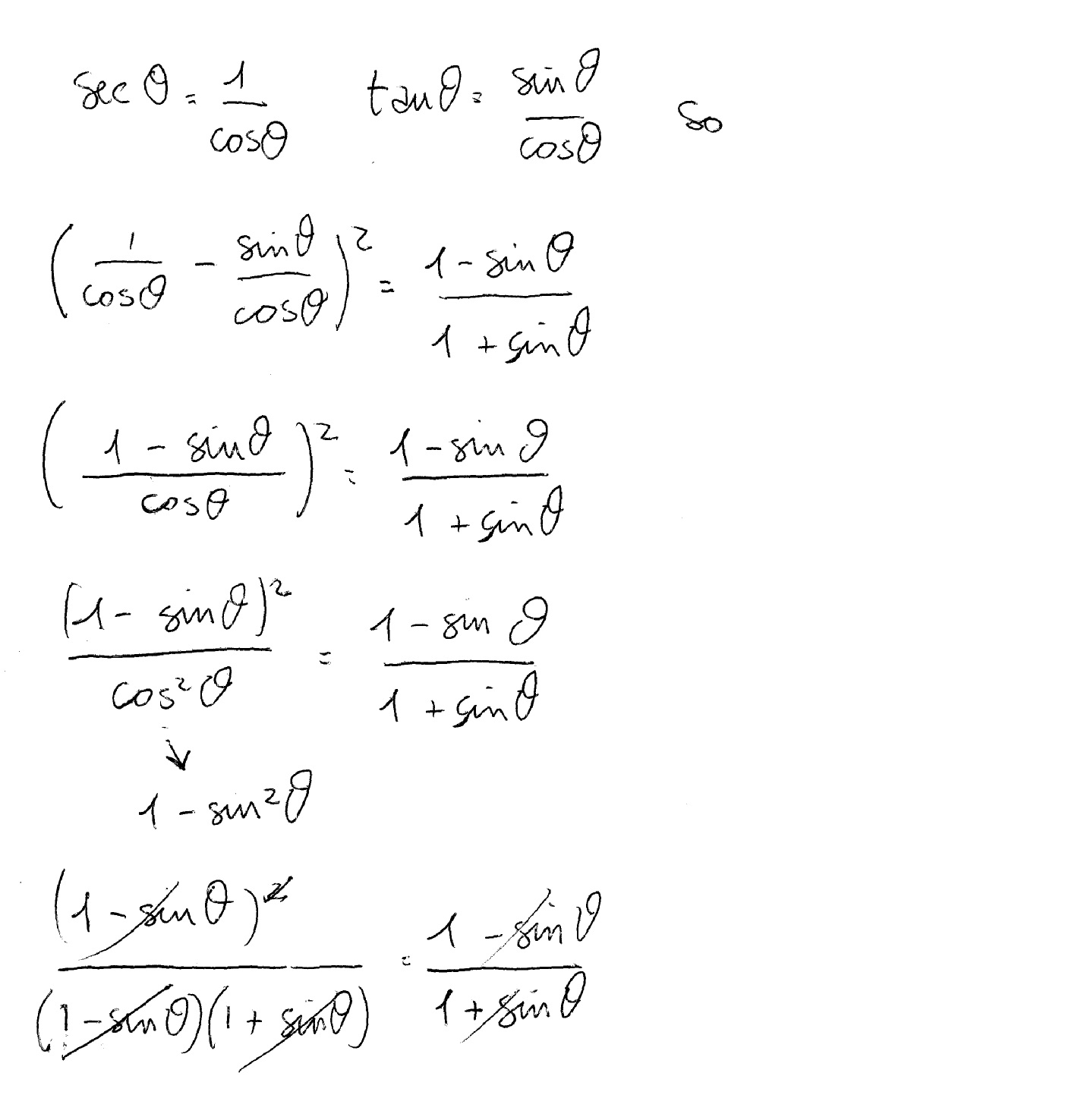


How Do You Prove The Identity Sectheta Tantheta 2 1 Sintheta 1 Sintheta Socratic
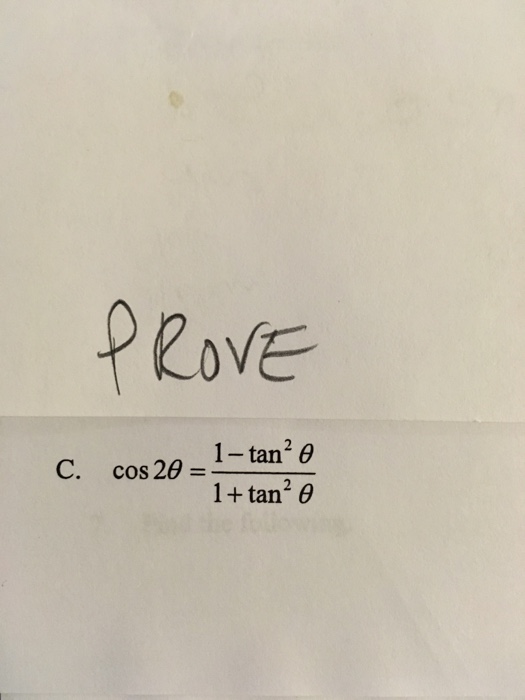


Solved Prove Cos 2 Theta 1 Tan 2 Theta 1 Tan 2 Theta Chegg Com



Prove That Tan Theta 1 Tan Theta Sec2 Theta Brainly In



1 Tan 2theta 1 Cot 2theta 1 Tan Theta 1 Cot Theta 2 Tan 2 Theta Brainly In


